암알못의 암호 핥기 - 치환암호

저번 글에서 고전 암호부터 현대 암호까지 대강 뭐가 있구나를 살펴봤습니다.

기술적인 내용은 딱히 없었는데요, 이번 편에서는 고전 암호 중 치환 암호를 좀 더 자세히 살펴보겠습니다.

1. 치환 암호 : 시저 암호

시저 암호(또는 카이사르 암호, Caesar cipher)는 간단한 치환암호입니다.

평문의 알파벳들을 각각 일정한 거리만큼 떨어진 다른 알파벳으로 치환하는 방식입니다.

#위키피디아 : Caesar Cipher

ABCEDF를 왼쪽으로 3씩 밀면 XYZABC가 된다.

시저 암호에서 암호키는 각 알파벳을 얼만큼 이동할 것이냐이고, 복호키는 그 반대입니다.

쉽네요!

직접 암호를 해독해봅시다!

wechall이란 사이트의 문제입니다.

Training: Crypto - Caesar I

XLI UYMGO FVSAR JSB NYQTW SZIV XLI PEDC HSK SJ GEIWEV ERH CSYV YRMUYI WSPYXMSR MW QGRJLRSKRKVS

(주의! 암호문과 정답은 매번 다릅니다)

시저 암호로 암호화된 문장이 주어졌습니다.

암호키는 주어지지 않는데요, 어떻게 풀까요? :)

암호키의 경우의 수를 생각해봅시다.

알파벳은 총 26개이니 암호키는 자신이 나오는 경우를 제외하고 25의 경우의 수를 가집니다.

많지 않으니 직접 해보면 될것 같습니다.

우리는 똑똑한 사람이니 코드를 짜도록 하겠습니다!!!

'''
WeChall
Training: Crypto - Caesar I
'''

import string

def shift(c, N):
    if c not in string.ascii_lowercase:
        return c
    if ord(c)+N > ord("z"):
        return chr( ord(c)+N - 26 )
    else:
        return chr( ord(c)+N )

def solve(chip):
    for i in range(1,26):
        mes = ''
        for c in chip:
            mes += shift(c,i)
        print "key("+str(i)+") : "+mes

if __name__ == '__main__':
    chip = raw_input('> ').lower()
    solve(chip)

간단한 코드입니다.

shift(c, N) 함수는 문자 c를 N만큼 오른쪽으로 시프트한 문자를 반환해주는 함수이고,

solve(chip) 함수는 암호키를 1씩 늘려가며 총 25번의 복호화를 시도하는 함수입니다.

실행결과, 알아볼 수 있는 문장 하나가 나옵니다! 저게 답 이겠네요.

암호화키는 오른쪽으로 22번 쉬프트였습니다.

혹시 이 문제를 풀면서 시저 암호의 특징을 발견하셨나요??

if c not in string.ascii_lowercase:
     return c

힌트는 이 코드입니다.

저는 문자 c가 소문자 알파벳(ascii_lowercase)가 아니라면 그 문자 그대로를 반환하도록 했습니다.

시저 암호의 암호화 대상에는 알파벳 이외의 문자나 숫자가 포함되지 않기 때문입니다.

시저 암호의 이러한 특징을 수정해서, 모든 ascii 문자를 암호화하는 문제가 있습니다!

이것도 한 번 풀어보도록 할게요.

Training: Crypto - Caesar II

53 7B 7B 70 20 76 7B 6E 38 20 05 7B 01 20 7F 7B

78 02 71 70 20 7B 7A 71 20 79 7B 7E 71 20 6F 74

6D 78 78 71 7A 73 71 20 75 7A 20 05 7B 01 7E 20

76 7B 01 7E 7A 71 05 3A 20 60 74 75 7F 20 7B 7A

71 20 03 6D 7F 20 72 6D 75 7E 78 05 20 71 6D 7F

05 20 00 7B 20 6F 7E 6D 6F 77 3A 20 63 6D 7F 7A

33 00 20 75 00 4B 20 3D 3E 44 20 77 71 05 7F 20

75 7F 20 6D 20 7D 01 75 00 71 20 7F 79 6D 78 78

20 77 71 05 7F 7C 6D 6F 71 38 20 7F 7B 20 75 00

20 7F 74 7B 01 78 70 7A 33 00 20 74 6D 02 71 20

00 6D 77 71 7A 20 05 7B 01 20 00 7B 7B 20 78 7B

7A 73 20 00 7B 20 70 71 6F 7E 05 7C 00 20 00 74

75 7F 20 79 71 7F 7F 6D 73 71 3A 20 63 71 78 78

20 70 7B 7A 71 38 20 05 7B 01 7E 20 7F 7B 78 01

00 75 7B 7A 20 75 7F 20 75 73 75 7F 78 75 7F 74

7F 78 7C 7F 3A

(주의! 암호문과 정답은 매번 다릅니다)

모든 ascii 문자를 포함하기 때문에 자신이 나오는 경우를 제외하고 경우의 수가 127로 늘어났습니다.

하지만 푸는 방법은 동일합니다.

'''
WeChall
Training: Crypto - Caesar II
'''

def shift(c, N):
    return chr( (ord(c)+N) % 128 )

def solve(chip):
    for i in range(1,128):
        mes = ''
        for c in chip:
            mes += shift(c,i)
        print "key("+str(i)+") : "+mes

def getChip(fname):
    fd = open(fname, "r")
    tmp = fd.read()
    tmp = tmp.split("\n")

    data = ''
    for line in tmp:
        hex_line = line.split(" ")
        for c in hex_line:
            if c is not " " and c is not "\n" and c is not '':
                data += chr(int(c,16))
    return data

if __name__ == '__main__':
    chip = getChip(raw_input('> '))
    solve(chip)

암호문의 입력 방식을 파일 입력으로 바꿨습니다.

해독의 범위를 늘려준 것 외에는 이전의 코드와 거의 동일합니다.

시저는 역시 시저.. 이번에도 정답을 찾아냈습니다!

암호키는 오른쪽으로 116번 쉬프트!

하지만 127개의 문장들을 훑어보려니 좀 귀찮죠?

Caesar I 문제를 푼 결과, 평문에 “solution” 이라는 문자가 들어가는 것을 추측해낼 수 있습니다.

이를 이용하여 출력 부분의 코드를

if "solution" in mes:
    print "key("+str(i)+") : "+mes

이렇게 바꿔주면

군더더기 없이 정답만 출력할 수 있습니다!

평문에 어떤 문자가 들어가는지 추측할 수 있는 상황에서 써먹을 수 있겠죠?

2. 치환 암호 : 단일 치환

시저 암호는 간단한 치환 암호라고 했습니다.

그럼 다른 치환 방법은 무엇이 있을까요?

시저 암호는 알파벳을 쉬프트 한 것이기 때문에 하나의 알파벳이 어떤 알파벳으로 바뀌는지에 따라 다른 알파벳들도 무엇으로 바뀔지 결정납니다.

하지만 쉬프트를 사용하지 않고 순서에 상관 없이 무작위의 한 알파벳과 1대 1 대응을 이룬다면 조금 더 복잡해지겠죠?

이렇게 1대 1 대응을 이루는 치환 방식을 단일 치환이라고 부릅니다.

암호화 키와 복호화 키는 대응된 알파벳 테이블이겠네요~

Training: Crypto - Substitution I

TU OGN QSPJCGOU CAR UAB KQL WNQR OGJH PU ZWJNLR J QP JPDWNHHNR INWU MNSS RALN UABW HASBOJAL YNU JH RWZKPQKDSGJW OGJH SJOOSN KGQSSNLCN MQH LAO OAA GQWR MQH JO

(주의! 암호문과 정답은 매번 다릅니다)

하.. 막막하네요..

총 25! 의 경우의 수가 있습니다.

시저 암호처럼 경우의 수를 모두 시도하면 풀 수 있을까요?

코드를 짜봅시다..

'''
WeChall
Training: Crypto - Substitution I
'''

import string
import itertools

def solve(chip):
    data = []
    for i in range(len(chip)):
        if chip[i] == ' ':
            data.append(ord(' '))
        else:
            data.append(ord(chip[i])-ord('A'))

    sub = itertools.permutations(string.ascii_uppercase, 26)

    for line in sub:
        plain = ''
        for i in range(len(chip)):
            if data[i] == 32:
                plain += ' '
            else:
                plain += line[data[i]]
        if " YOU " in plain or " SOLVE " in plain or " THE " in plain or " SOLUTION " in plain:
            print "[line]"
            print line
            print "plain"
            print plain

if __name__ == '__main__':
    chip = raw_input('> ')
    solve(chip)

itertools를 사용하여 모든 경우의 수를 구하고, 평문에 들어있을만한 문자들을 추측했습니다.

…

후….

매우 느립니다.

다른 방법은 없을까요?ㅠ

암호문을 다시 봅시다.

TU OGN QSPJCGOU CAR UAB KQL WNQR OGJH PU ZWJNLR J QP JPDWNHHNR INWU MNSS RALN UABW HASBOJAL YNU JH RWZKPQKDSGJW OGJH SJOOSN KGQSSNLCN MQH LAO OAA GQWR MQH JO

이번엔 문자열의 특징을 생각해볼까요?

치환 암호는 1대 1로 변환되기 때문에 문자열의 특징이 그대로 반영됩니다.

문자열이 가진 정보는 빈도 정보 등이 있는데요, 빈도 정보는 많이 사용되는 알파벳과 적게 사용되는 알파벳 정보를 말합니다.

빈도 수를 분석해서 알파벳의 대응 관계를 쉽게 추측해 나갈 수 있습니다.

# 빈도수 통계 그래프

영어 문자열에서 가장 많이 나타나는 알파벳은 “e”라고 하는데요,

암호문에서 많이 나타나는 알파벳이 있다면 그 알파벳은 “e”라고 생각해볼 수 있는 것입니다.

그럼 우리의 암호문에서 빈도수를 체크해봅시다!

'''
WeChall
Training: Crypto - Substitution I
bindo su check
'''

su = dict()

def cnt(t):
    return t[1]

def printBindo():
    sort_su = sorted(su.iteritems(), key=cnt, reverse=True)
    for i in sort_su:
        print i[0] + " : " + str(i[1])

def bindo(chip):
    for i in range(len(chip)):
        if chip[i] in su:
            su[ chip[i] ] += 1
        else:
            su[ chip[i] ] = 1

if __name__ == '__main__':
    chip = raw_input('> ').upper()
    bindo(list(chip))
    printBindo()

스페이스바를 제외하면 “N”이 가장 많이 나왔네요!

빈도수 통계 그래프를 참고하여 쉽게 평문을 구할 수 .. 사실 저는 여기서 감이 잘 오지 않았습니다.

빈도수 통계 그래프에 의하면 “e”가 눈에 띄게 많고 그 외의 알파벳들은 비슷비슷한 것들이 많습니다.

문자열의 가진 특징으로는 알파벳의 빈도수 외에도 단어의 빈도수를 생각할 수 있는데요,

안타깝게도 자주 등장한다고 할 만한 단어는 없습니다.

그나마 “OGJH”와 “MQH”가 2번씩 등장했는데요,

자주 쓰이는 단어이면서 단어 안에 겹치는 알파벳이 없는 3-4 글자의 단어를 생각하자면 떠오르는 것이 “THE”와 “THIS” 정도가 있습니다.

그 중에서 “OGJH”를 “THIS”로 치환하면

“THIS”라는 단어 외에 “THE”와 “IS”라는 단어가 추가로 나타난 것을 확인할 수 있었습니다.

“OGJH”가 “THIS”일 확률이 조금 더 올라갔네요!

이제부터는 각 단어의 패턴을 추측해야하는데요,

제 눈에 제일 먼저 들어오는 익숙한 패턴은 “S_TI”(암호문 : HASBOJAL)입니다.

이전의 문제들의 답에는 항상 “SOLUTION”이라는 단어가 들어갔었는데 패턴이 일치하죠?

이제부턴 쉽습니다. 이런식으로 단어의 패턴을 추측하다보면 평문을 구할 수 있습니다!

이 암호문의 경우 저는 (SOLUTION -> CHALLENGE -> WAS -> AM -> IMPRESSED -> ALMIGHTY -> VERY -> FRIEND -> BY -> KEY) 순으로 알아냈습니다.

빈도 정보는 조금 힘드네요

빈도 정보를 이용한 암호의 특징을 눈치 채셨나요?

위의 문제를 풀면서 빈도 정보를 추출했을 때 난감했던 문제가, 빈도 정보들이 비슷비슷한 것이었습니다.

즉, 문장이 길어지면 길어질 수록 빈도 정보가 확실해지고 암호문을 풀기도 좀 더 수월해 질 것입니다.

암호화 대상을 확장해서 다시 풀어봅시다~

Training: Crypto - Substitution II

B5 13 83 E0 BF F2 FD 8D E3 F2 FD F1 13 83 33 59

6A DB 24 F1 33 6A 13 83 D0 6A 12 F2 33 6A 24 F2

BF 5C D0 BF B9 6A 37 8D FD 6A FB 13 8D 6A E0 13

FD 6A F1 FD 59 6A 2C D0 BF FB 6A 12 D0 E3 E3 6A

5C 13 83 D0 6A 21 D0 E3 E3 13 12 6A 24 F2 F0 BE

D0 BF 59 6A DB 24 D0 6A 8F BF 13 37 E3 D0 6C 6A

12 F1 FD 24 6A FD 24 F1 33 6A F0 F1 8F 24 D0 BF

6A F1 33 6A FD 24 F2 FD 6A FD 24 D0 6A BE D0 FB

6A F1 33 6A 8F BF D0 FD FD FB 6A E3 13 83 E0 59

6A 45 6A 12 F1 E3 E3 6A F0 13 6C D0 6A 8D 8F 6A

12 F1 FD 24 6A F2 6A 37 D0 FD FD D0 BF 6A D0 83

F0 BF FB 8F FD F1 13 83 6A 33 24 D0 6C D0 6A F2

83 FB 6A 33 13 13 83 59 6A 10 13 8D BF 6A 33 13

E3 8D FD F1 13 83 6A F1 33 67 6A 6C F0 21 13 13

37 F2 37 F0 BF E3 6C 59

대소문자 구분 됨, 구두 점 사용

(주의! 암호문과 정답은 매번 다릅니다)

이번에는 ascii 문자 뿐만 아니라 0xff까지 문자의 범위가 늘어났습니다.

힌트가 되는 것이라면 대소문자가 구분된다는 것과 구두점을 사용한다는 것입니다.

구두점은 보통 마지막에 찍으니 0x94가 구두점이겠네요.

구두점을 기준으로 살펴보면 마지막 구두점을 제외하고는 0xD6이 따라오고, 제일 많은 빈도수를 가지고 있습니다.

이 문자는 스페이스바로 추측됩니다

구두점과 스페이스바를 구하면 첫 번째 문장이 15글자의 단어로 끝나는 것을 볼 수 있습니다.

제일 먼저 생각난 단어는 “Congratulations” 였습니다.

들어맞은 것 같네요!

“Congratulations”를 구한 것 만으로도 많은 글자들이 나타났습니다.

여기서부터는 단어의 패턴을 이용하여 이전 문제와 동일하게 풀면 됩니다 :D

분명 N글자의 단어인데 한 글자가 더 붙어있다면 기호일 가능성을 의심해보세요(저는 이것 때문에 헤맸습니다ㅠ)

이렇게 하나의 문자가 다른 하나의 문자로 치환되는 것을 단일 치환이라고 하는데요, 문자의 특성이 그대로 반영되기 때문에 빈도 정보를 이용할 수 있었습니다.

이러한 문제점을 발견하여 빈도 정보를 무력화시키는 다중 치환 방식이 등장했습니다.

3. 치환 암호 : 다중 치환, 비제네르 암호

다중 치환 방식을 사용하여 암호화하면 같은 알파벳이더라도 다른 알파벳으로 치환될 수 있습니다.

다중 치환을 사용하는 암호로는 대표적으로 비제네르(Vigenere) 암호가 있는데,

비제네르 암호를 통해 다중 치환을 알아봅시다!

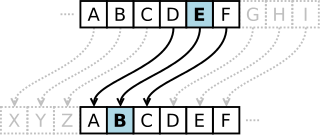
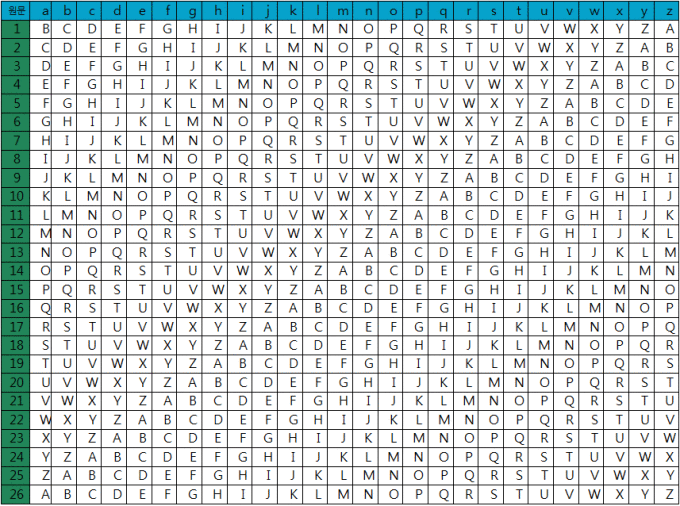
비제네르 암호(비제네르, 비즈네르, 비그니어 .. 다양하게 읽습니다)는 행렬 표를 이용하여

평문의 문자인 x와 암호화 키의 문자 y를 행렬 표의 x행 y열에 있는 문자로 치환합니다.

비제네르 암호의 행렬표

# 위키 백과 : 비즈네르 암호

평문이 “vigenere”이고 암호화 키가 “bpsec”이라면 비제네르 행렬표에 의해 “wxyipfgw”로 암호화됩니다.
이때 똑같은 문자인 ‘e’에 대해서 각각 ‘i’, ‘f’, ‘w’로 치환된 것을 확인할 수 있습니다.

비제네르 암호는 카지스키 분석법과 프리드만 암호 공격을 이용해서 복호화가 가능합니다.

카지스키 분석법의 핵심은 “암호문에 반복적으로 나타나는 단어의 간격”입니다.

암호문이 충분히 길다면 그 안에 특정 문자열이 반복해서 나타날 수 있습니다.

예를 들어, “cat”이라는 단어가 반복적으로 들어간 평문을 암호화 했을 때,

“cat”이라는 단어에 대응되는 암호화 단어는 서로 다를 수도 있지만 반복되는 단어이다보니

키가 맞아떨어져서 같은 단어가 나올 수도 있습니다.

[키]

l egen dsl eg en d slegen dsl e gen ds le gen dsleg e ndsl ege nd sl e gendsl ege n dsl eg en dsl egend s lege nds le ge n dslege nds l ege nd sl ege ndsle

[평문]

i love cat it is a pretty cat a cat is on the table i love cat it is a pretty cat a cat is on the table i love cat it is a pretty cat a cat is on the table

[암호문] t puzr fse mz mf d hcizxl fse e feg lk zr zlr wsmpk m yrnp ggx vw ad e vvrwlj ggx n fse my sa wzp xgfyh a wsui pdl tx ow n sjpxzc pdl l ggx vv gy xni gdtwi

(암호문이 충분히 길고 반복되는 단어가 많을 수록 정확합니다)

위의 예시에서는 14의 간격(‘f’에서 ‘f’까지의 거리)과 42의 간격으로 같은 단어가 반복되었습니다.

이때 우리는 키의 길이가 14의 약수라고 생각할 수 있지만,

키에 사용된 단어나 우연에 의해 “cat”이 아닌 다른 단어가 “fse”로 암호화될 수도 있습니다.

여기에 프리드만 암호 공격을 같이 사용하면 거의 정확하게 키의 길이를 알아낼 수 있습니다.

프리드만 암호 공격의 핵심은 “암호문에서 임의로 두 문자를 선택했을 때 두 문자가 서로 같을 확률(일치 지수)“입니다.

단일 치환 암호의 경우, 평문에서 ‘a’라는 알파벳의 일치 지수는 암호문에서 ‘a’에 대응되는 알파벳의 일치 지수와 동일합니다.

다중 치환 암호의 경우는 빈도 정보를 균등화했으므로 일치 지수가 감소하게 됩니다.

여기서 중요한 것은 키 길이에 따라 감소하는 정도가 달라진다는 것입니다.

이때문에 암호문에서의 일치지수를 조사하여 키 길이를 알아낼 수 있습니다.

수학적인 증명 과정을 통해 나온 최종 수식은 다음과 같습니다.

이 수식 또한 암호문이 길어질 수록 정확도가 올라갑니다.

아까의 예제에 적용시켜봅시다!

최종적으로 5.193377 이라는 근사값이 나왔는데요,

카지스키 분석법으로 알아낸 키 길이 후보는 14의 약수인 2, 7, 14 였는데

이 중 수식 값과 가장 가까운 7이 키 길이인 것을 알 수 있습니다.

키 길이를 알아냈다면 암호문을 키 길이 만큼으로 나누고,

같은 문자의 키로 암호화 된 부분들을 모아 빈도수를 분석하며 키를 알아내면 됩니다.

아래는 암호문을 분석하여 프리드만의 수식 결과를 출력해주는 파이썬 코드입니다.

'''
Vigenere - Friedmann
'''
import re

su = dict()

def cnt(t):
    return t[1]

def bindo(chip):
    data = list(chip)
    for i in range(len(chip)):
        if data[i] in su:
            su[ data[i] ] += 1
        else:
            su[ data[i] ] = 1

def calc_I(chip):
    n = len(chip)
    tmp = 0
    for c in su.iteritems():
        tmp += c[1]*(c[1]-1)
    return float(tmp)/(n*(n-1))

def calc_l(chip):
    n = len(chip)
    return (0.027*n) / ( (n-1)*calc_I(chip) - 0.038*n + 0.065 )

if __name__ == '__main__':
    chip = raw_input('> ').upper()
    chip = re.sub(r'\s+', '', chip)

    bindo(chip)
    print calc_l(chip)

마무리

• 단일 치환 암호
  1. 1대 1 치환 암호
  2. 빈도 정보를 통해 복호화가 가능하다. (알파벳, 단어 등의 빈도 수)
  3. 암호문이 길수록 복호화가 쉬워진다.

• 예시 : 시저 암호
  1. 평행 이동
  2. 경우의 수를 모두 시도해봄으로써 복호화가 가능하다.

• 다중 치환 암호
  1. 하나의 평문 알파벳에서 여러 암호 알파벳이 나올 수 있다.
  2. 빈도 정보를 통해 복호화가 가능하다. (알파벳, 단어 등의 빈도 수)
  3. 암호문이 길수록 복호화가 쉬워진다.

• 예시 : 비제네르 암호
  1. 카지스키 분석법과 프리드만 암호 공격을 통해 복호화가 가능하다.
  2. 암호키의 길이를 알면 빈도 정보를 활용하여 복호화가 가능하다.

고전 암호 중 치환 암호에 대해서 알아봤습니다.

저는 공부를 위해 문제를 풀면서 필요한 프로그램을 직접 작성 했는데요, 암호를 해독해주는 좋은 툴들이 많습니다.

원리를 아셨다면 이미 있는 좋은 툴들도 사용해보세요 :)

다음 편에서는 전치 암호에 대해 알아보겠습니다!