By rls1004 | December 6, 2016
암알못의 암호 핥기 - 비대칭키 암호

마지막! 비대칭키 암호 :)
대칭키 암호는 하나의 키로, 암호화와 복호화가 가능하므로 키 관리가 굉장히 중요하다고 했습니다.
암호화된 통신을 할 두 사용자가 하나의 비밀키를 공유해야 하기 때문에, 비밀키 전달 과정에서 키가 외부에 노출될 위험이 있습니다.
이번 편에서 다룰 비대칭키 암호는 공개키를 이용해 암호화하고 공개키에 해당하는 비밀키를 이용해 복호화하는 방식입니다.
내 공개키를 상대방에게 알려주면 상대방은 공개키를 이용해 데이터를 암호화하고, 암호화된 데이터를 나에게 보냅니다.
암호화된 데이터는 내가 갖고 있는 개인키를 이용해 복호화할 수 있습니다.
반대로 내가 상대방에게 데이터를 보낼 때는 상대방이 알려준 공개키를 이용해 암호화하고,
상대방은 자신이 갖은 비밀키를 사용해 복호화합니다.
즉, 전달되는 것은 공개키 뿐인데 공개키 만으로는 데이터를 복호화할 수 없습니다.
비대칭키 암호는 공개키를 사용한다고 해서 공개키 암호라고도 합니다.
비대칭키 암호의 대표적인 예로는 RSA, 타원 곡선 암호, 전자 서명 등이 있습니다.
RSA 알아보기
비대칭키 암호 중에서도 가장 유명한(?) RSA(Rivest, Shamir and Adleman) 암호를 알아보겠습니다.
RSA 알고리즘은 크게 세 단계로 나뉩니다.
키 생성, 암호화, 복호화.
키 생성
먼저 공개키와 개인키를 생성하는 방법입니다.
두 개의 큰 소수인 p와 q를 선택합니다.
p = 13, q = 17
p와 q의 곱인 N을 계산합니다.
N = p * q = 13 * 17 = 221
1부터 N-1 까지의 정수 중 N과 서로소인 정수의 개수를 구합니다.
서로소란 두 숫자의 최대 공약수가 1이 되는 수를 말합니다.
N이 소수라면 N과 서로소인 정수는 N-1개, N이 소수의 곱이라면 N과 서로소인 정수는 (p-1) * (q-1) 이 됩니다.
이 값을 N에 대한 오일러 파이(φ) 함수 값이라고 합니다.
φ(N) = (p-1) * (q-1) = (13-1) * (17-1) = 192
1 < e < φ(N) 이고 φ(N)과 서로소인 공개키 e를 생성합니다.
1 < e < 192,
e = 7 로 생성해봅시다.
(d * e) mod φ(N) = 1 이고 0 <= d <= N 인 d를 구합니다.
(d * e) mod φ(N) = 1, (d * 7) mod 192 = 1,
d = 55 로 선택해봅시다.
생성된 값들 중 N과 e는 공개키로, d는 비밀키로 사용됩니다.
암호화
암호화 방법도 생각보다 어렵지 않습니다.
M은 평문, C는 암호문, N과 e는 공개키입니다.
C = Me mod N
M = 123, N = 221, e = 7
C = 1237 mod 221 = 98
복호화
복호화에는 비밀키인 d가 사용됩니다.
M = Cd mod N
C = 98, N = 221, d = 55
M = 9855 mod 221 = 123
너무 간단한데요..?
겁먹었던 것과는 다르게 알고리즘이 꽤 단순합니다.
N과 e는 공개되는 값이니 N을 소인수분해하면 p와 q를 구할 수 있고,
공개키 e와 두 소수 p, q를 이용하여 개인키 d를 얻을 수 있습니다!
…하지만 말처럼 간단하면 RSA 암호가 널리 쓰일 수 없었겠죠?
RSA 암호는 안전성을 보장하기 위해 적어도 1024 bit 길이의 키 값을 사용하고, 현대에는 2048 bits 를 권장하고 있습니다.
8 bit 소인수 분해하기!
78 = 2 *3 * 13
1024 bit 소인수 분해하기!
132833671401188681409933195937192629016976319629594795799131992
764447145859868597380583367096816957136866531150247169175959451
441991292762067544772161126493382599978606541478038120180495085
039244683156982582458932869310068299882234630366425035860646225
88755070341711043414628011397488535003670047463628509100 = …?
보다시피, 키 길이가 길어질 수록 소인수 분해는 힘들어집니다.
Brute Force 공격을 시도할 경우에도 상당히 많은 시간이 필요합니다.
(768 bit 의 RSA key 를 알아내는 데에는 100대에 가까운 컴퓨터가 연결된 클러스터로 2년이 걸렸다고 하네요!)
또, RSA 알고리즘을 살펴보면 modular(%) 연산이 등장하는데요,
192 mod 191 의 연산 값은 1로 매우 구하기 쉽지만 X mod 191 = 1 에서의 X 값은 찾기 어렵습니다.
192, 383, 574, … 가능한 값이 너무 많거든요 :(
이렇게 한 방향으로는 값을 구하기 쉽지만 역 방향으로는 값을 구하기 어려운 함수를 일방향 함수라고 합니다.
modular 연산은 소인수 분해를 더욱 어렵게 하는 요소로 쓰였습니다.
정리해보면, 공개키를 이용해 개인키를 알아내기는 매우 어렵다는 얘깁니다 :0
Ekoparty CTF
개념은 어느정도 익힌 것 같으니, 문제를 풀어보겠습니다!
2015년 Ekoparty CTF 에 출제된 RSA 2070 이라는 문제입니다.
Recover the private key and the flag.
Hint : Check your padding
주어진 파일은 공개키인 public.key와 암호화된 데이터인 flag.enc 파일입니다.
public.key 파일의 내용은 아래와 같은데요,
—–BEGIN PUBLIC KEY—–
MIIBJDANBgkqhkiG9w0BAQEFAAOCAREAMIIBDAKCAQMlsYv184kJfRcjeGa7Uc/4
3pIkU3SevEA7CZXJfA44bUbBYcrf93xphg2uR5HCFM+Eh6qqnybpIKl3g0kGA4rv
tcMIJ9/PP8npdpVE+U4Hzf4IcgOaOmJiEWZ4smH7LWudMlOekqFTs2dWKbqzlC59
NeMPfu9avxxQ15fQzIjhvcz9GhLqb373XDcn298ueA80KK6Pek+3qJ8YSjZQMrFT
+EJehFdQ6yt6vALcFc4CB1B6qVCGO7hICngCjdYpeZRNbGM/r6ED5Nsozof1oMbt
Si8mZEJ/Vlx3gathkUVtlxx/+jlScjdM7AFV5fkRidt0LkwosDoPoRz/sDFz0qTM
5q5TAgMBAAE=
—–END PUBLIC KEY—–
공개키는 숫자인데 base64로 인코딩된 듯한 문자와 위아래로 텍스트 문자열이 들어가있죠?
이러한 형태를 띄고 있는 파일은 PEM(Privacy Enhanced Mail) 포맷 파일로, 공개키를 암호화한 파일입니다.
직접 base64 디코딩을 해줘도 되지만 키값이 아닌 데이터도 포함되어 있기 때문에
정확한 키를 알아내기 위해 openssl 이라는 툴을 사용하겠습니다.
openssl은 네트워크를 통한 데이터 통신에 쓰이는 TLS와 SSL 프로토콜을 구현하는 오픈소스 라이브러리로,
인증서 확인 및 키 생성 등의 기능을 제공하고 있습니다.
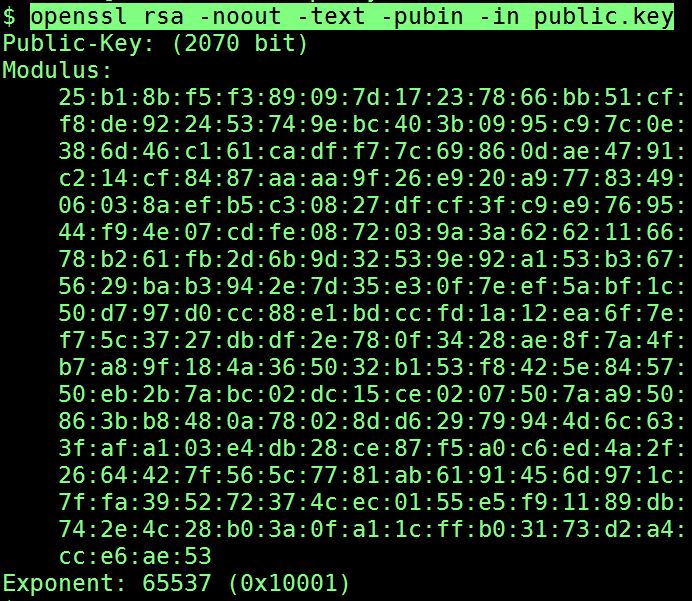
rsa라고 알고리즘을 지정해주고, -noout -text 옵션으로 PEM 인코딩된 인증서를 파싱해서 정보를 출력해줍니다.
이렇게 출력된 값이 바로 공개키입니다!
공개키 중 N은 2070 bit를 사용하고 있고, e는 65537 이라는 값입니다.
N을 알았으니 이제 p와 q를 구해야겠죠? (N = p * q)
2070 bit 를 brute force 하기에는 무리인데.. 마침 좋은 사이트가 있습니다!
위 사이트는 소인수분해에 대한 데이터 베이스를 갖고 있는 사이트입니다.
소인수분해를 하고 싶은 숫자를 입력했을 때 데이터 베이스에 있는 값이라면 결과를 출력해줍니다.
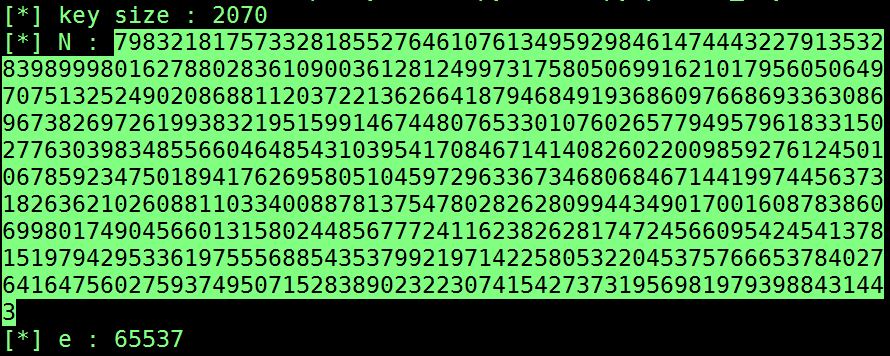
일단 N 값을 파싱하고..
'''
RSA Algorithm
2015 Ekoparty CTF Quals - RSA 2070
Parsing N
'''
import sys
s_keysize = "Public-Key: ("
e_keysize = " bit)"
s_n = "Modulus:\n"
e_n = "\nExponent"
s_e = "Exponent: "
e_e = " (0x"
def getSize(data):
start = data.find(s_keysize) + len(s_keysize)
end = data.find(e_keysize)
return int(data[start:end])
def getN(data):
start = data.find(s_n) + len(s_n)
end = data.find(e_n)
line = data[start:end].split("\n")
N = "0x"
for one in line:
one = one.split(" ")[1]
one = one.split(":")
for num in one:
N += num
return int(N,16)
def getE(data):
start = data.find(s_e) + len(s_e)
end = data.find(e_e)
return int(data[start:end])
if __name__ == "__main__":
f_name = sys.argv[1]
fd = open(f_name, "r")
data = fd.read()
size = getSize(data)
print "[*] key size : %d" % size
N = getN(data)
print "[*] N : %d" % N
e = getE(data)
print "[*] e : %d" % e
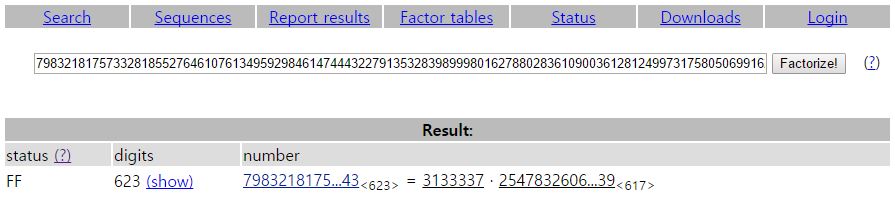
N 값을 factordb 에서 검색해봅시다.
798321817573328185527646107613495929846147444322791353283989
998016278802836109003612812499731758050699162101795605064970
751325249020868811203722136266418794684919368609766869336308
696738269726199383219515991467448076533010760265779495796183
315027763039834855660464854310395417084671414082602200985927
612450106785923475018941762695805104597296336734680684671441
997445637318263621026088110334008878137547802826280994434901
700160878386069980174904566013158024485677724116238262817472
456609542454137815197942953361975556885435379921971422580532
204537576665378402764164756027593749507152838902322307415427
37319569819793988431443 = 3133337 *
254783260649374192922001721363994977190818429145282283164559
062116931183219713999360047291348411629741442462714864396957
860365881174246118819559509962196468073788222782856382615820
991083394389495730341012151411561564087428438200480668308638
143623798857203950823184628500029016056897618763191511473527
300909575569408421442998873946787436077669378280944783364011
594490358783068537162165483742734623865083073677131120730040
113834189678949305540675824532489810220119228833744427368480
459206763413618712317871634414675330768900817218821793691687
872877247696426653999925560521448458786001262839688902730675
75342061776244939
무시무시한 결과네요.. 두 개의 소수가 나왔습니다!
이렇게 발견된 두 개의 소수, p와 q를 가지고 rsatool를 이용하면 비밀키인 d를 생성할 수 있습니다.
rsatool.py -o private.key -p 3133337 -q
254783260649374192922001721363994977190818429145282283164559
062116931183219713999360047291348411629741442462714864396957
860365881174246118819559509962196468073788222782856382615820
991083394389495730341012151411561564087428438200480668308638
143623798857203950823184628500029016056897618763191511473527
300909575569408421442998873946787436077669378280944783364011
594490358783068537162165483742734623865083073677131120730040
113834189678949305540675824532489810220119228833744427368480
459206763413618712317871634414675330768900817218821793691687
872877247696426653999925560521448458786001262839688902730675
75342061776244939
PEM 형식의 비밀키 생성에 성공했습니다!
비밀키를 알았으니 이제 복호화할 수 있겠죠?
openssl을 사용해서 복호화를 해봅시다~
(python -c ‘import sys,base64; sys.stdout.write(base64.decodestring(open(“flag.enc”,“r”).read()))’) > d_flag.enc
우선 flag 파일을 base64 디코딩 해서 준비하고,
openssl을 사용하여 복호화해줍니다!
복호화할 파일은 -in 옵션을 사용하여 지정해주고, -inkey 옵션으로 아까 생성한 비밀키를 지정해줍니다.
그리고 RSA 알고리즘은 같은 평문에 대해 동일한 암호문이 생성되는 단점이 있어
이를 보완하기 위한 난수 패딩(OAEP, Optimal Asymmetric Encryption Padding)이 사용되기도 하는데,
이 문제의 경우가 OAEP 가 적용된 암호문입니다.( 위로 올라가서 문제의 Hint를 보면 padding이 적용된 것을 알 수 있습니다! )
그러므로 -oaep 옵션을 사용합니다.
flag : EKO{classic_rsa_challenge_is_boring_but_necessary}
RSA의 한계..?
RSA는 공인인증서나 SSL 등에서도 사용되는 알고리즘입니다.
키 길이가 충분하고 개인키를 잘 보관한다면 안전하다고 알려져있는데요,
키 길이가 짧을 경우는 N을 소인수분해하여 p와 q를 구하는게 가능하고 이를 통해 비밀키를 구할 수 있게 됩니다.
또, 키 길이가 짧을 경우 암호문을 반복해서 암호화하면 평문이 나오기도 합니다.
공개키와 암호문만으로 평문을 구하는 방법인데요,
N = 13 * 17 = 221, e = 7, C = 123 일 때,
Me mod N = C
1237 mod 221 = 98
987 mod 221 = 123
개인키 없이도 암호문을 복호화할 수 있습니다.
이 외에는 암호화와 복호화에 시간이 많이 걸린다는 단점이 있습니다. SSL에서는 이를 보완하기 위해 대칭키 방식을 함께 사용합니다.
또, RSA는 brute force 공격이 거의 불가능하다고 했는데,
이것도 컴퓨터의 성능이 발전하고, 양자 컴퓨터가 나온다면 안전성이 떨어질 수밖에 없겠죠?
그때를 대비하여 RSA를 대체할 양자 암호 기술 개발에도 관심이 증가하고 있습니다.
마무리
드디어 <암알못의 암호핥기> 시리즈의 마지막편이 끝났습니다!
암호는 제 생활과 거리가 좀 멀어보이고 모른채로 지내도 상관 없을 것 같다는 생각이 초기의 생각이었는데요,
암호학에 대해 공부하면서 보니 저는 평소에도 암호를 충분히 접하고 있다는게 느껴지더라구요.
어렵고 다가갈 수 없는 느낌이었는데 조금은 친숙해진 것 같습니다:)
<암알못> 시리즈를 봐주셔서 감사합니다!